The TL;DR key points
2. Know our biases, such as overconfidence and availability biases 3. Use statistics, even simple ones
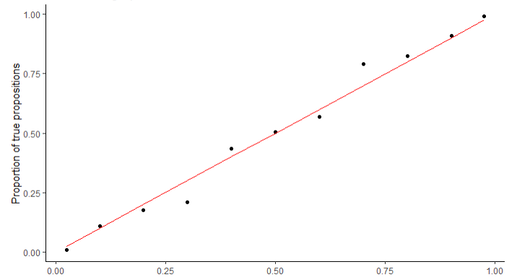
Estimating risk: Why you should care about itNowadays, we’re especially worried about risks—about the risk of getting COVID if we hop on a plane or go to an in-person class, or about the risk of dying if we get COVID. And some risks are worth taking, but others aren't; it depends partly on how we estimate the risks. So, then, how good are we at estimating risk? And how should we estimate risks? Below, I’ll share some ideas on these questions. These aren’t just my personal thoughts, though. Instead, they’re based on decades of psychological and scientific research, including cutting-edge research programs funded by the US intelligence community. Now I don’t specialize in "risk" per se. I specialize in probability and psychology. But we might think that a "risk" simply is a kind of probability: it’s the probability of something bad happening. Of course, we could argue endlessly over how to interpret the word “probability”. But this isn’t really the issue we care about here. Instead, what we want to know is how confident we should be that various bad things might happen. This is what we can call "risk estimation". So I’ll discuss two things: what makes us bad at estimating risk, and what’ll make us much better at it. The hope is that we can use this to improve our lives—to help us feel more confident about what decisions to make and to feel no more or less worried than we need to be. I'll group my ideas under three pointers. Here's the first: 1. Think in terms of probabilityWhen it comes to estimating risk, we want to know how confident we should be that something bad might happen—how confident you can be that you’ll get COVID if you take a flight, for instance. We can represent this confidence with a number—a percentage between 0% and 100%. We could say this number is a kind of "probability", like so-called Bayesians do. At first, this might seem counter-intuitive: how could I assign a probability to a unique event, like the risk of me getting COVID if I take this specific flight on this specific day? And this is a reasonable question: if we think about it enough, almost any event is unique in a myriad ways, and it might seem strange that we could assign probabilities to these unique events. However, some pioneering research from the US intelligence community offers some surprising insight (Mellers et al., 2015). One of their most remarkable findings is that some people can assign probabilities like this and, when they do, they have good "calibration", as it's called. Calibration “Calibration” here is a technical term. We would say you have good calibration just in case anything you assign a probability of 80% to happens about 80% of the time, anything you assign a probability of 70% to happens about 70% of the time, and so forth. For instance, if you're well calibrated, it'd rain 80% of the time when you say there's an 80% probability of rain. It turns out that some people are well calibrated like this, even when it comes to unique events. For example, in one research program funded by the US intelligence community, one person made 1,056 probability estimates about events over the course of one year. These were estimates about events like international conflicts, pandemics, elections and the like. I used data from the program to quickly produce a rough graph which shows how calibrated this person was: What does this graph mean? Well, the horizontal x-axis represents the probabilities which they attached to events, each grouped into categories close to 10%, 20%, 30% and so forth. The vertical y-axis represents the number of times that the events in the category happened. The straight line represents what someone would look like if they were perfectly calibrated. It shows that as someone would assign higher probabilities to events, the more frequently those events occur. And the dots here represent how calibrated this particular person was. You can see the dots are pretty close to the line: when this person assigned a probability of 80% to an event, that event happened about 83% of the time. And when they assigned a probability of 90% to an event, that event happened about 91% of the time. And this isn't an accident. This person improved their calibration over time, as is often the case. The remarkable thing about this is that, in a sense, all of these events were unique. They concerned things such as, for example, the probability that the "Libyan government forces regain control of the city of Bani Walid before 6 February 2012". Now that's pretty unique: we're talking about a specific government, with specific forces, regaining control of a specific city by a specific time. Despite the fact that this is clearly a unique event, this individual was well calibrated when making estimates about this and countless other unique events. The moral of the story is that it’s possible for us to assign probabilities to even unique events, and we can be well calibrated in doing so. And this is handy because we often can’t know whether something bad will happen: we can only be more or less confident, and representing this confidence with a number is useful to get a sense of how worried we should be or which risks are worth taking and which aren’t. However, as we'll see, we’re often pretty bad at assigning these numbers—but we can get better! And here's how. 2. Know your biasesIn general, many people aren’t that good at estimating probabilities, and unless someone's done special training or research on the topic, they could be one of them. Of course, the good news is that people can improve! And I’ll share some thoughts on this below. But for now, let us delve into the bad news in more detail, in part because we’re better thinkers when we understand and expand our limits than when we don't. Overconfidence Let’s take as our cue the studies of overconfidence. “Overconfidence” here is another technical term. It happens when you assign a higher probability to something than the frequency with which that thing is true. For example, if someone assigns a probability of 80% something, and it turns out that that thing is true only 60% of the time, then they’re overconfident—and by 20% in this case. Unfortunately, overconfidence is almost everywhere. For example, in one study, they asked 100 students questions that tested their general knowledge about such things as whether a leopard is faster than a gazelle (Lechuga & Wiebe, 2011). The results found that the students were overconfident: out of all the things they assigned a probability of 95% or more to, only 73% of those things were true. (BTW, fun fact: it turns out that it's false that a leopard is faster than a gazelle... the average gazelle is nearly twice as fast... so much fun.) And unfortunately, overconfidence is present even where we might least expect it. One study examined the calibration of 189 experts whose job it was to give opinions about political affairs—the outcomes of wars, elections and the like (Tetlock, 2005). The study looked at the calibration of their long-term predictions which they were certain about—that is, the things they assigned a probability of 100% to. How many of those things happened? Well, only 81% of them. Put differently, when they were completely certain something wouldn't happen, it actually did happen 19% of the time. That's pretty bad, especially since their job is to give opinions—and the media and other organizations often rely on those opinions! Having a PhD or having many years of experience didn't make a difference either. The situation is also bad when we look at medicine. One study found that 118 doctors were generally overconfident (Meyer et al., 2013). They were asked to give diagnoses about easier cases where 55.3% of the diagnoses were right. And they were also asked to give diagnoses about harder cases where only 5.8% of the diagnoses were right. That might not be so worrying. What is more worrying, though, is that the doctors were similarly confident about their diagnoses in both kinds of cases: they were about as confident in themselves when they were likely to be wrong as when they were likely to be right. This isn't trivial; it impacts real people's lives and is sometimes a matter of life and death. As Professor of Medicine Robert Watcher says, "Today in America, hundreds of patients will be falsely reassured and panicked, and many of them will be medicated, scanned and even cut open because of the wrong diagnosis" (TriMed Staff, 2006). One might think—or at least hope—that I am cherry picking studies here: perhaps these are just a few unfavorable studies and people aren't really that bad when it comes to probabilities. I wish that were the case, but the fact of the matter is that there is so much evidence of overconfidence that I could have a whole paragraph just of references to it and similar phenomena. In fact, here it is: (Barnsley et al., 2004; Berner & Graber, 2008; Callender et al., 2016; Ehrlinger et al., 2008; Gilovich et al., 2002; Hall et al., 2016; Kruger & Dunning, 1999; Lechuga & Wiebe, 2011; Lundeberg et al., 2000; Meyer et al., 2013; Miller Tyler M. & Geraci, 2011; Naguib et al., 2019; Neyse et al., 2016; Perel et al., 2016; Podbregar et al., 2001; Tetlock, 2005; Tirso et al., 2019; Whitcomb et al., 1995; Wright et al., 1978; Yates et al., 1989, 1996, 1997, 1998) ... that's with the abbreviations included. And even then, there's more evidence that I can't be bothered citing. You get the gist. Findings like this led Mellers et al. (2015) to say, “Across a wide range of tasks, research has shown that people make poor probabilistic predictions of future events ” (266). But if that's the case, we shouldn't expect to be so good at predicting risks either. Heuristics: Availability Why, then, might we be so bad at estimating risk? To answer this question, we can look at how we often arrive at our judgments in the first place. That’s where the so-called heuristics come in. “Heuristics” are simply processes by which we arrive at conclusions—conclusions about risks or other things. They’re often quick and efficient, but they can also produce biased judgments, especially when it comes to estimating risk. Let’s take the availability heuristic, for example. We use the availability heuristic when we estimate the risk of something based on the ease with which that thing comes to our mind. We equate the probability of something with the "mental availability" of that thing, as it were. For example, you might think there’s a high risk of getting COVID if you take a flight, merely because you can easily recall stories of people getting COVID when they took a flight. Or you might think there’s a high risk that you’ll die if you get COVID, merely because you can easily recall a story of someone like you who died of COVID. The problem with the availability heuristic, though, is that the availability of something often isn’t the same as the probability of that thing. For instance, one study found people thought that the risk of a random person dying from a flood was higher than the risk of them dying from asthma (Lichtenstein et al., 1978). At the time, though, the reverse was true: 9 times as many people died from asthma as they did from floods. People likewise overestimated the risk of other “sensational” events like homicides, tornadoes, car accidents, cancer and the like. Some scholars blame the media for this (Reber, 2017). They claim the news excessively covers dramatic stories, and this makes the risks appear greater than they really are. The result is a lot of overconfidence about risks and a lot of unnecessary worry. If we’re to accurately estimate risks, then, it seems that we need to ask ourselves how we’re estimating risk and whether we’re biased by such things as availability. And of course, other things can bias our judgments and lead to inaccuracy, but I don't want to bore you with details more than I already have. In any case, often our biases can be reduced with another little tip: 3. Use statistics!So, what do you do if you want to know the risk of something? Well, we can look at some statistics! We’re often afraid of numbers, but we don’t need to be. Even simple statistics can be informative, and our ability to use them well is a litmus test for the accuracy of our estimates. So how do we use these statistics? Well, if you want to know the risk of something, maybe try looking at the relevant proportion of the time that that thing happens. The Probability of Getting COVID on a plane For example, you want to know the risk of getting COVID if you take a flight? Then maybe look at how many people on flights get COVID. Statistics like this are often available, and it sometimes takes just a little searching to find them. Here, it turns out we have those statistics for one place at least--New Zealand! There, everyone who arrives in the country is placed in managed isolation and is tested. This includes people from countries around the world: India, Australia and the United States, for example. Since March 26, it turns out that 344 people tested positive. Now, these people were spread across 113 flights. Probably at least one person on each of those flights had to have COVID to begin with. So we can plausibly conclude that out of those 344 people, at most only 231 people on those flights got infected from others on board. (Even then, the true number is probably much lower than that.) So what does this estimate of 231 mean? Well, nothing until we consider the total number of people who arrived in the country in the first place. Since March 26, over 26,400 people have flown into New Zealand. So our toy estimate is that 231 out of 26,400 people got COVID from flights—not even 1% of them. We could also look at the data from another angle, focusing on more recent arrivals. As of July 6th, about 6,000 people were in managed quarantine, virtually all of whom arrived into New Zealand within the 14-days previous to that. During that time, only 23 people tested positive, and they were spread across 8 flights. We could then use that to form a toy estimate that at most 15 out of 6,000 got COVID on their flight, about 0.25%. What's more, if we look at the data over time, we'll see there's always been a low number of infected people on these flights. So what inference should we draw from this? Here’s my suggestion: that the risk is very low. And how exactly do we draw this inference? Well, there’s different ways to do it, some of which are more complicated than others. The simple way is just to draw an intuitive inference in accordance with what is known as the straight-rule (Reichenbach, 1949). To do this, we just take our estimate that 0.9% of people got infected, and we conclude that the probability you'll get COVID from a flight is about 0.9%. Put differently: you can be more than 99% confident that you won't get COVID if you take a flight—at least if you're as precautious as the average Joe. Simple intuitive inferences like this can sometimes get us into trouble if we don’t consider how big our sample of people is, among other things. But in this specific case, the available evidence suggests this way of assigning probabilities is no less accurate than any other. However, some statisticians would still hate it if you did that, and they’d hate me for saying you could do that. Instead, they'd recommend you use more complicated statistical methods for drawing inferences, and I've included a very boring appendix* on how you might do that. But no matter what way you look at it, the risk is very small. And it is doubtful that most other flights are that different either—for now at least. Conclusions: Making Estimates, and Taking Risks If we think statistically in this way, then our risk estimates will be more accurate. But "more accurate" estimates don't mean the "most accurate" estimates. We can often refine our estimates in various ways: by considering statistics from other sources, by analyzing the data in different ways, by looking at more of the specific features of the thing we're estimating, and so on and so forth. We also need to be aware of changes that should affect our estimates, such as outbreaks in areas which we might be flying from. But in some cases, crude calculations like this are sufficiently accurate, and hopefully this is at least a simple illustration of the type of statistical thinking that is indispensable to accurate risk estimation. You might ask, though: how do we know that statistical thinking like this makes us more accurate? Well, because we know that this is the kind of thing that the best thinkers do—those people who are in the minority of well calibrated reasoners (Chang et al., 2017; Tetlock & Gardner, 2015). But I suspect that if we thought this way, we often wouldn't worry as much as we do, especially people who worry about what'll happen if they get COVID when they're not in "at risk" categories. Of course, some of us are "at risk" and should worry about COVID more than we do. But I think we'd all agree that it's important to strike a balance. Accurate risk estimation helps us to do that. However, correctly "estimating" a risk is not the same as correctly "taking" a risk. Nothing in this post tells you about what risks you should take. Theories in ethics and rational decision theory tell us about that—like utilitarianism. So this doesn't mean we should be reckless. We might still think we have ethical obligations to be precautious out of respect for vulnerable populations, for instance, even if we don't feel the need to be precautious for ourselves. But the moral of the story is that risks are everywhere, and we're often bad at estimating them—but we can get better! And when we do, we might find ourselves less worried about life—but hopefully in a conscientious way :) I'll discuss more about what makes for good judgment in future posts. But if you want to learn more about probabilistic prediction now, you might like to check out Good Judgment’s training. There, you’ll find cutting-edge training about how to make predictions about future events. These are often events about political topics—like wars and elections. However, the basic principles of probabilistic reasoning are arguably generalizable to other contexts—or so I’d argue if I had more space. UPDATE 7/15/2020: My friend Jonathan Ammaral has just brought to my attention an interesting article here. It reports a study of over 1,500 adults. They found that younger adults overestimate the risk of dying from COVID-19 by as much as 10 times.
Using similar logic to the above, lots of young people can be even more confident than 99.8% that they won't die if they get COVID. There are several reasons for this:1) fatality rates are lower than this in several other countries which they might be in, 2) benign COVID cases are often undercounted and undetected, thereby inflating the reported fatality rate, and 3) out of the very small minority of young people who pass away, many have health conditions which predispose them to complications--such as diabetes and the like--and many young people can be confident that they don't have these conditions. In saying that, some young people do have these health conditions and are quite rightly concerned for their wellbeing, so I think we should all do our part for their sake. *A very boring appendixAbove, I mentioned that you might use the straight-rule to be more than 99% confident that you won't get COVID if you take a flight. However, some statisticians would hate me for saying you could do that. Instead, they’d recommend more complicated methods of drawing inferences. Which one they’d recommend depends on whether they’re a “Bayesian”, or a “frequentist”, or something else. Unfortunately, though, there’s bitter debates between these camps of statisticians, and I don’t want to go to war by siding with one camp against the other. So I’ll just point out what happens if we use different methods, but you don’t need to worry the details here. If you’re a Bayesian, then you could do inference in different ways. Technically, the simple "straight-rule" inference above is compatible with a Bayesian approach. But some Bayesians might insist that you should do some kind of “population parameter estimation”, where the parameter in this case is something like the "true proportion" of people who get infected on flights, or the "objective propensity" of such infection. To do this estimation, you could do “Bayesian conditionalization” using a “uniform prior probability distribution" over the "parameter space” and a “binomial distribution” for the “likelihoods of the sample data”. This would yield a “posterior probability distribution” over the “parameter space” which you could use to do “posterior predictive inference”. If you did all of that, the probability you’d get COVID on a flight is still around 1%—basically a pompous version of the simple inference above. But if you’re a frequentist, then you’d probably do “confidence interval estimation” instead. One way of doing this would generate a “99% confidence interval” of [0.0073, 0.0103]. This means that the method of generating this interval would generate intervals which contain the true "parameter value" 99% of the time when that method is applied to a series of "hypothetical data sets". When applied to the sample estimate, that same method then yields an interval of [0.0073, 0.0103]. So how confident should you then be that you’ll get COVID if you take a flight? To be honest, I don’t know the answer, even though people frequently misinterpret confidence intervals as telling you the answer (Hoekstra et al., 2014). Frequentism doesn’t explicitly tell you anything about how confident you should be. It just tells you about specific kinds of “probabilities” that are interpreted as “frequencies” instead of degrees of confidence. But I'm guessing any frequentist would say you should be quite confident you wouldn’t get COVID on board anyways, even if frequentism doesn’t tell you this. Either way, it looks to me like statisticians in all camps would say the risk is low. End of boring appendix. Some light bedtime reading for you...
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
AuthorJohn Wilcox Archives
January 2023
Categories
All
|
 RSS Feed
RSS Feed